Given:
The table of values of a linear relationship.
x y
-1 -1
0 1
1 3
2 5
To find:
The equation for the given table of values.
Solution:
If a linear function passes through the two points, then the equation of the linear relationship is
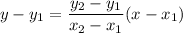
Consider any two point from the given table. Let the two points are (-1,-1) and (0,1). So, the equation of the linear relationship is
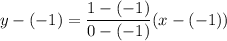
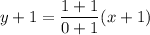


Using distributive property, we get
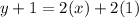
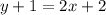
Subtracting 1 from both sides, we get
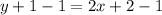
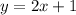
Therefore, the required equation is
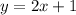 . Hence, the correct option is D.
. Hence, the correct option is D.