Question

Use an induction proof to prove this statement:
For n≥1, 4^n+5 is divisible by 3.

Answer 1

See below

Explanation:

We shall prove that for all
`n\in\mathbb{N},3|(4^n+5)`. This tells us that 3 divides 4^n+5 with a remainder of zero.

If we let
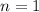`n=1`, then we have
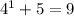`4^(1)+5=9`, and evidently,
`9|3`.

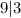Assume that
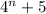`4^n+5` is divisible by
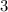`3` for
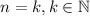`n=k, k\in\mathbb{N}`. Then, by this assumption,
`3|(4^n+5)\Rightarrow4^k+5=3m,\: m\in\mathbb{Z}`.

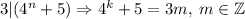Now, let
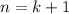`n=k+1`. Then:

`4^(k+1)+5=4^k\cdot4+5\\=4^k(3+1)+5\\=3\cdot4^k+4^k+5\\=3\cdot4^k+3m\\=3(4^k+m)`

Since
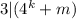`3|(4^k+m)`, we may conclude, by the axiom of induction, that the property holds for all
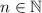`n\in\mathbb{N}`.