Question

A regulation soccer field for international play is a rectangle with a length between 100 m and a width between 64 m and 75 m. What are the smallest and largest areas that the field could be?

Answer 1

the largest areas that the field could be is
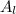`A_l`=7587.75 m

the smallest areas that the field could be is
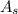`A_s`=6318.25 m

Step-by-step explanation:

to the find the largest and the smallest area of the field measurement error is to be considered.

we have to find the greatest possible error, since the measurement was made nearest whole mile, the greatest possible error is half of 1 mile and that is 0.5m.

therefore to find the largest possible area we add the error in the mix of the formular for finding the perimeter with the largest width as shown below:

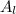`A_l`= (L+0.5)(W+0.5)

(100+0.5)(75+0.5) = (100.5)(75.5) = 7587.75 m

To find the smallest length we will have to subtract instead of adding the error factor value of 0.5 as shown below:

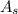`A_s`= (L-0.5)(W-0.5)

(100-0.5)(64-0.5) = (99.5)(63.5) = 6318.25 m

Answer 2

The smallest and largest areas could be 6400 m and 7500 m, respectively.

Step-by-step explanation:

The area of a rectangle is given by:

`A = l*w`

Where:

l: is the length = 100 m

w: is the width

We can calculate the smallest area with the lower value of the width.

`A_(s) = 100 m*64 m = 6400 m^(2)`

And the largest area is:

`A_(l) = 100 m*75 m = 7500 m^(2)`

Therefore, the smallest and largest areas could be 6400 m and 7500 m, respectively.

I hope it helps you!