Question

Recall the equation for a circle with center (h, k) and radius r. At what point in the first quadrant

does the line with equation y = 2x + 4 intersect the circle with radius 3 and center (0, 4)?

Answer 1

`\displaystyle \Big((3√(5))/(5),(6\sqrt5)/(5)+4\Big)`

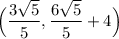
Explanation:

Recall that the equation for a circle is given by:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius.

Then for a center of (0, 4) and a radius of 3, our equation is:

`x^2+(y-4)^2=9`

We want to know at what point does the circle intersect with the line:

`y=2x+4`

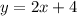
Therefore, we can solve for x. To do so, substitute the linear equation into the circle equation:

`x^2+((2x+4)-4)^2=9`

Simplify:

`x^2+(2x)^2=9`

Square:

`x^2+4x^2=5x^2=9`

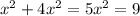
Divide both sides by 5:

`\displaystyle x^2=(9)/(5)`

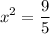
Therefore:

`\displaystyle x=\pm(3)/(√(5))=\pm(3√(5))/(5)`

In QI, x is always positive, so we only need to consider the positive case:

`\displaystyle x=(3√(5))/(5)`

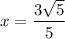
Using the linear equation again, we can see that:

`\displaystyle y=2\Big((3√(5))/(5)\Big)+4=(6√(5))/(5)+4`

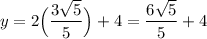
Therefore, the point in which a circle with center (0, 4) and a radius of 3 intersects the line with equation y = 2x + 4 in the first quadrant is the point:

`\displaystyle \Big((3√(5))/(5),(6\sqrt5)/(5)+4\Big)`

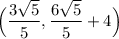
Or approximately:

`\approx (1.342, 6.683)`

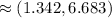
And we are finished!