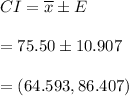Question

A supervisor records the repair cost for 22 randomly selected VCRs. A sample mean of $75.50 and standard deviation of $18.07 are subsequently computed. Determine the 99% confidence interval for the mean repair cost for the VCRs. Assume the population is approximately normal. Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.

Answer 1

The t value for 99% CI for 21 df is 2.831.

The critical value that should be used in constructing the confidence interval is (64.593, 86.407).

Explanation:

Now the sample size is less than 30 and also population standard deviation is not known.

Then we will use t distribution to find CI

t value for 99% CI for 21 df is TINV(0.01,21)=2.831

The margin of error is
`E=t*(s)/(√(n))\\\\=2.831*(18.07)/(√(22))\\\\=10.907`

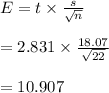
Hence CI is
`CI=\overline{x} \pm E\\\\ =75.50 \pm 10.907\\\\=(64.593,86.407 )`