Question

Suppose lifetime of certain type of car batteries are

normally distributed. Brand G has a mean lifetime of three years and

a standard deviation of one year. Brand M has a mean lifetime of 36

months and a standard deviation of four months.

(a) Which brand is more reliable and why?

(b) Pick one battery from each brand randomly, which one has a

better chance to last for four years and why?

Answer 1

Follows are the solution to the given points:

Explanation:

The brand (M) will become more reliable as the standard deviation of an (M) brand will be much lower than the standard deviation of (G) brand.

such as four years,

Calculating the z score for G brand
`= ((4-3))/(1) = (1)/(1) = 1`

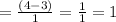
Calculating the z score for M brand
`= ((4-3))/(((1)/(3))) = ((1))/(((1)/(3))) = 1 * (3)/(1)= 3.`

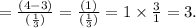
Because the z mark of the (G) brand is less, it is much more probable that the (G) Brand could last four years. It is because the variability of the (G) brand is very high, which allows lasting longer by expanding its expansion.