Answer: The height of one propeller tip is 3.68 feet when t= 3.5 minutes.
Explanation:
Given: The height of one propeller tip as a function of time is given by
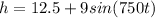 ), where h is the height in feet and t is the time in minutes.
), where h is the height in feet and t is the time in minutes.
Put t = 3.5 , we get
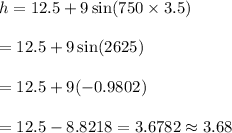
Hence, The height of one propeller tip is 3.68 feet when t= 3.5 minutes.