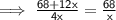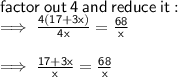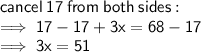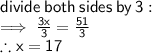Answer:

Explanation:
to understand this
you need to know about:
- equation
- equation word problems
- PEMDAS
given:
- Miguel can drive 4 times as fast as Raul can ride his bicycle. If it takes Raul 3 hours longer than Miguel to travel 68 miles, how fast (in mph) can Raul ride his bicycle
tips and formulas:
to find
- how fast can Raul ride his bicycle
let's solve:
let's the speed of Raul be x
likewise
Miguel can drive 4 times as fast as Raul can ride his bicycle
therefore
4x
according to the question