Question

MC Qu. 82 A design engineer wants to construct a sample... A design engineer wants to construct a sample mean chart for controlling the service life of a halogen headlamp his company produces. He knows from numerous previous samples that this service life is normally distributed with a mean of 500 hours and a standard deviation of 20 hours. On three recent production batches, he tested service life on random samples of four headlamps, with these results: Sample Service Life (hours) 1 495 500 505 500 2 525 515 505 515 3 470 480 460 470If he uses upper and lower control limits of 520 and 480 hours, what is his risk (alpha) of concluding servicelife is out of control when it is actually under control (Type I error)? A. 0.0026B. 0.0456C. 0.3174D. 0.6826E. 0.9544

Answer 1

B) 0.0456

Step-by-step explanation:

It is given that :

Rationale :

UCL = 480

LCL = 480

∴ Mean ,
`$\bar X = 500$`

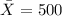
The standard deviation of sample (Sn) = 11.55

Z (for UCL)
`$=\frac{\text{UCL - Mean}}{\text{Sn}}$`

`$=(520-500)/(10)$`

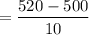
= 2

Similarly,

Z (for LCL)
`$=\frac{\text{LCL - Mean}}{\text{Sn}}$`

`$=(480-500)/(10)$`

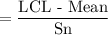
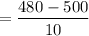
= -2

Now using the z table for finding the confidence level between Z value of -2 and 2.

Confidence level = 0.4772 + 0.4772

= 0.9544

Risk (alpha) = 1 - confidence level

= 1 - 0.9544

= 0.0456