Question

1. The nominal rate on Sandra's loan is 7.125%. If the interest is compounded monthly, what rate of

interest is Sandra actually paying? (use the formula)

Answer 1

She is actually paying a rate of 7.36% of interest.

Explanation:

The real interest rate, as a decimal, is given by:

`I = (1 + (r)/(n))^(n)`

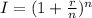
In which r is the interest rate and n is the number of compoundings during an year.

The nominal rate on Sandra's loan is 7.125%, compounded monthly:

This means that
`r = 0.07125, n = 12`

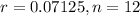
So

`I = (1 + (0.07125)/(12))^(12) = 1.0736`

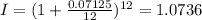
As a percentage: 1.0736*100 = 107.36% - 100% = 7.36%

She is actually paying a rate of 7.36% of interest.