Question

Solve
f(x)=4x5−8x4+8x2−4x

Answer 1

Given:

The function is:

`f(x)=4x^5-8x^4+8x^2-4x`

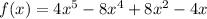
To find:

The roots of the given equation.

Solution:

We have,

`f(x)=4x^5-8x^4+8x^2-4x`

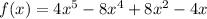
For roots,
`f(x)=0`.

`4x^5-8x^4+8x^2-4x=0`

`4x(x^4-2x^3+2x-1)=0`

`4x((x^4-1)+(-2x^3+2x))=0`

`4x((x^2+1)(x^2-1)-2x(x^2-1))=0`

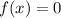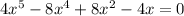
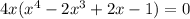
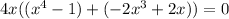
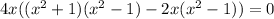
On further simplification, we get

`4x(x^2+1-2x)(x^2-1)=0`

`4x(x-1)^2(x+1)(x-1)=0`

`4x(x+1)(x-1)^3=0`

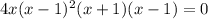
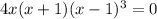
Using zero product property, we get

`4x=0`

`x=0`

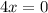
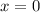
Similarly,

`x+1=0`

`x=-1`

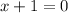
And,

`(x-1)^3=0`

`x=1`

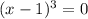
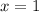
Therefore, the zeroes of the given function are
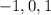`-1,0,1` and the factor form of the given function is
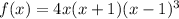`f(x)=4x(x+1)(x-1)^3`.