Question

(a) Write

`{2}^(5) / {2}^(5)`
as a single power if 2.
​

Answer 1

2^0

Explanation:

When you are dividing 2 exponents with the same base (in this case, 2) you subtract them. 2^5 ➗ 2^5 => 2^(5-5) = 2^0 => which is equal to 1, but the answer here would be 2^0.

Answer 2

There are two ways to go about this problem.

The first way, the generic way, is to know that,

`(a^n)/(a^m)=a^(n-m),a\\eq0`.

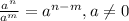So,

`(2^5)/(2^5)=2^(5-5)=\boxed{2^0}`.

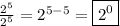The second way is to realise that both numerator and denominator are equal and when diving two equal numbers you obtain 1. (except when diving zeros) aka,

`(a)/(a)=1, a\\eq0`

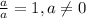
And 1 equals to any number raised to the power of zero,

`a^0=1,a\\eq0`

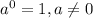
So we just have to say that the 1 we got is rewritten as some base to the power of zero.

Since our base needs to be 2, we just simply say,

`2^0`.

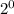Et Viola.

Hope this helps.