Question

A container has 20 12 cups of pancake mix. A serving uses exactly 2 ) cups.

Part A
How many full servings are in the container?
full servings
(a)
Part B
How many cups of pancake mix are left over?

Answer 1

10 full servings and
`(1)/(4)` cups leftover

Explanation:

Our container has a total of 20 and a half cups. And each full serving is 2 cups.

So, we divide
`(20(1)/(2) )/(2)`.

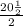To do this manually, we convert the numerator into an improper fraction:
`((41)/(2) )/(2)`.

Now, we multiply the denominators:
`(41)/(4)`.

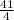This will give us
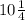`10(1)/(4)` servings. So we only have 10 full servings.

There are
`(1)/(4)` cups leftover.