Question

Rami bought a house on 1st January 2015. In2015 the house increased in value by 15%. In 2016 the house decreased in value by 8%. On 1st January 2017 the value of the house was $687700. What was the value of the house on 1st January 2015

Answer 1

The value of the house on 1st January 2015 was of $650,000.

Explanation:

Decimal multipliers:

For a increase of a%, the decimal multiplier is given by
`(100+a)/(100)`

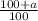
For a decrease of a%, the decimal multiplier is given by
`(100-a)/(100)`

Rami bought a house on 1st January 2015.

For a value of x.

In 2015 the house increased in value by 15%.

This means that x is multiplied by
`(100+15)/(100) = (115)/(100) = 1.15`

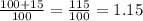
In 2016 the house decreased in value by 8%.

This means that 1.15 times x is multiplied by
`(100-8)/(100) = (92)/(100) = 0.92`

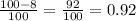
On 1st January 2017 the value of the house was $687700.

The value of these multiplications is 687700.

What was the value of the house on 1st January 2015?

This is x, so:

`x*1.15*0.92 = 687700`

`x = (687700)/(1.15*0.92)`

`x = 650000`

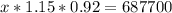
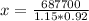
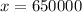
The value of the house on 1st January 2015 was of $650,000.