Answer:
a.) X ≈ N (0, 12)
b.) Y ≈ exp(2)
c.) The given distribution is not defined.
d.) Not a standard form of any distribution .
Explanation:
Given - In parts (a)−(d) below, either use the information given to determine
the distribution of the random variable, or show that the information
given is not sufficient by describing at least two different random
variables that satisfy the given condition.
To find - (a) X is a random variable such that Mₓ(t) =
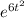 when |t| < 2.
when |t| < 2.
(b) Y is a random variable such that
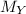 (t) =
(t) =
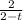 for t < 0.5.
for t < 0.5.
(c) Z is a random variable such that
 (t) = ∞ for t ≥ 5.
(t) = ∞ for t ≥ 5.
(d) W is a random variable such that
 (2) = 2
(2) = 2
Proof -
a.)
As we know that the moment generating function of normal distribution is given by
Mₓ(t) =
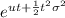
Now,
Mₓ(t) =
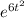
=
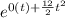
⇒μ = 0, σ = 12
Nd it is represented by
X ≈ N (0, 12)
b.)
Moment generating function of exponential function is given by
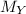 (t) =
(t) =
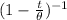
Now,
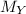 (t) =
(t) =
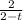 for t < 0.5.
for t < 0.5.
=
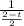
=
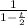
=
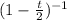
And it is represented by
Y ≈ exp(2)
c.)
Z is a random variable such that
 (t) = ∞ for t ≥ 5.
(t) = ∞ for t ≥ 5.
The given distribution is undefined.
d.)
 (2) = E(
(2) = E(
 )
)
=
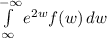
= 2
It is not the standard form of any distribution.