Question

A simple random sample of 8 reaction times of NASCAR drivers is selected. The reaction times have a normal distribution. The sample mean is 1.24

sec with a standard deviation of 0.12 sec. Construct a 99% confidence interval for the population standard deviation

Answer 1

99% confidence interval is 0.07 < σ < 0.32

Explanation:

Given that;

standard deviation s = 0.12 sec

s² = 0.12² = 0.0144

degree of freedom DF = n - 1 = 8 - 1 = 7

99% confidence interval

∝ = 1 - 99% = 1 - 0.99 = 0.01

now, we find x² critical values for ∝/2 = 0.005 and 1 - ∝/2 = ( 1 - 0.005) = 0.995, df = 7

The Lower critical value
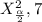`X^(2)_{(\alpha )/(2)},7` = 20.2777

The Upper critical value
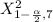`X^(2)_{1-{(\alpha )/(2)},7` = 0.9893

Now, confidence interval is given by

√[ ( (n-1)×s² ) / (
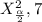`X^(2)_{(\alpha )/(2)},7` ) ] < σ < √[ ( (n-1)×s² ) / (
`X^(2)_{1-{(\alpha )/(2)},7` ) ]

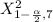so we substitute

√[ ( 7×0.0144 ) / ( 20.2777 ) ] < σ < √[ ( 7×0.0144 ) / ( 0.9893 ) ]

√[ ( 7×0.0144 ) / ( 20.2777 ) ] < σ < √[ ( 7×0.0144 ) / ( 0.9893 ) ]

√0.0049711 < σ < √0.10189

0.0705 < σ < 0.3192

Rounding to the nearest 2 decimal places

0.07 < σ < 0.32

Therefore; 99% confidence interval is 0.07 < σ < 0.32