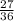Answer:
a.)
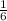
b.)
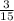
c.)
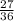
Explanation:
Given - We roll two fair 6-sided dice. If a fair dice is rolled, the probability
of it landing on any number between [1-6] is equi- probable
(i.e.,
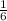 ).
).
To find - (a) Find the probability that doubles are rolled.
(b) Given that the roll results in a sum of 6 or less, and
the conditional probability that doubles are rolled.
(c) Find the probability that the larger of the two die's outcomes
is at least 4.
Proof -
As given , two fair 6-sided dice is rolled.
The sample space is as follows :
S = { (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) }
Total number of outcomes = 36
a.)
Sample space that double are rolled = { (1, 1), ( 2, 2), ( 3, 3) , ( 4, 4), ( 5, 5), ( 6, 6) }
Total number of possible outcomes = 6
So, Probability =
 =
=
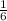
b.)
Sample space that roll shown sum of 6 or less = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1)}
Now,
Total outcomes = 15
Total possible outcome that doubles are rolled = 3 ( i.e (1,1), (2, 2), (3, 3) )
So, Probability =
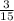
c.)
Sample space that larger of the two die's outcomes is at least 4 = { (1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) }
Total possible outcomes = 27
So, Probability =