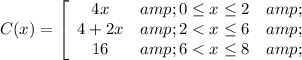Question

Write the piecewise defined function for the total cost of parking in the garage. That is, state the function C(x), where x is the number of hours a car is parked in the garage.

Answer 1

`C(x) = \left[\begin{array}{ccc}4x &0 \le x \le 2& \\4 +2x &2 < x \le 6& \\16 &6<x\le 8& \end{array}\right`

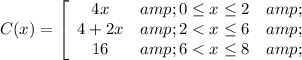
Explanation:

Given

See attachment for question

Required

The piece-wise function

From the attachment, we have:

(1) $4/hr for first 2 hours

This is represented as:

`C(x) = 4x`

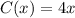
The domain is:
`0 \le x \le 2`

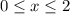
(2) $2/hr for next 4 hours

Here, we have:

`Rate = 2`

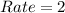
The total cost in the first 2 hours is:

`C(x) = 4x`

`C(2) = 4*2 = 8`

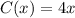
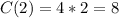
So, this function is represented as:

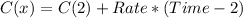`C(x) = C(2) + Rate * (Time - 2)` ----- 2 represents the first 2 hours

So, we have:

`C(x) = C(2) + Rate * (Time - 2)`

`C(x) =8 + 2(x - 2)`

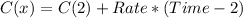
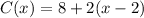
Open brackets

`C(x) =8 + 2x - 4`

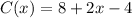
Collect like terms

`C(x) =8 - 4+ 2x`

`C(x) =4+ 2x`

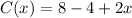
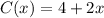
The domain is:

`2 < x \le 2 + 4`

`2 <x \le 6`

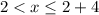
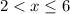
(3) 0 charges for the last 2 hours

The maximum charge from (2) is:

`C(x) =4+ 2x`

`C(6) = 4 + 2*6`

`C(6) = 4 + 12`

`C(6) = 16`

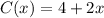
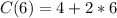
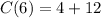
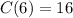
Since there will be no additional charges, then:

`C(x) = 16`

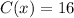
And the domain is:

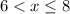`6 < x \le 8` --- 8 represents the limit

So, we have:

`C(x) = \left[\begin{array}{ccc}4x &0 \le x \le 2& \\4 +2x &2 < x \le 6& \\16 &6<x\le 8& \end{array}\right`