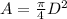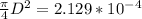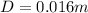Question

You have been assigned the task of reviewing the relief scenarios for a specific chemical reactor in your plant. You are currently reviewing the scenario involving the failure of a nitrogen regulator that provides inert padding to the vapor space of the reactor. Your calculations show that the maximum discharge rate of nitrogen through the existing relief system of the vessel is 0.5 kgls, However, your calculations also show that the flow of nitrogen through the l-in supply pipe will be much greater than this. Thus under the current configuration a failure of the nitrogen regulator will result in an over pressuring of the reactor. One way to solve the problem is to install an orifice plate in the nitrogen line, thus limiting the flow to the maximum of 0.5 kg/s. Determine the orifice diameter (in cm) required to achieve this flow. Assume a nitrogen source supply pressure of 15 bar absolute. The ambient temperature is 25°C and the ambient pressure is 1 atm. 3.

Answer 1

`D=0.016m`

Step-by-step explanation:

From the question we are told that:

Discharge Rate
`F_r=0.5kgls`

Pressure
`P=15Kpa`

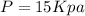
Temperature
`T=25=>298K`

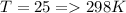
Ambient pressure is 1 atm.

Generally the equation for Density is mathematically given by

`\rho=(PM)/(RT)`

`\rho=(15*10^5*28.0134*10^(-3))/(8.314*298)`

`\rho=16.958kg/m^2`

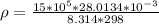
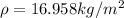
Generally the equation for Flow rate is mathematically given by

`F_r=\mu A\sqrt{Q \rho P((2)/(Q+1))^{(Q+1)/(Q-1)}}`

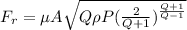
Where

`Q=Heat coefficient\ ratio\ of\ Nitrogen`

`Q=1.4`

`\mu= Discharge\ coefficient`

`\mu=0.68`

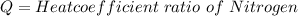
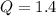
Therefore

`0.5=0.68 A\sqrt{1.4 16.958 15*10^(5)((2)/(1.4+1))^{(1.4+1)/(1.4-1)}}`

`A=2.129*10^(-4)`

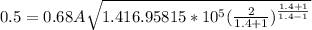
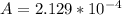
Where

`A=(\pi)/(4)D^2`

`(\pi)/(4)D^2=2.129*10^(-4)`

`D=0.016m`