Question

Sea un cuadrado de 2 pulgadas de lado uniendo los puntos medios se obtiene otro cuadrado inscrito en el anterior si repetimos este proceso obtenemos una progresión de infinitos cuadrado comprobar que la área de los infinitos cuadrados forman una progresión geométrica y calcula la suma de todas las áreas

Answer 1

1) La serie geométrica formada es

4, 2, 1,..., ∞

2) La suma al infinito de las áreas de los cuadrados es 8 in.²

Explanation:

1) El área del primer cuadrado, a₁ = 2² = 4 pulgadas²

El área del siguiente cuadrado, a₂ = (√ (1² + 1²)) ² = (√2) ² = 2 pulg²

El área del siguiente cuadrado, a₃ = ((√ (2) / 2) ² + (√ (2) / 2) ²) = 1 pulg²

Por lo tanto, la razón común, r = a₂ / a₁ = 2/4 = a₃ / a₂ = 1/2

Las áreas de los cuadrados progresivos forman una progresión geométrica como sigue;

4, 4×(1/2), 4 ×(1/2)²,...,4×
`(1/2)^(\infty)`

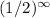
De donde obtenemos la serie geométrica formada de la siguiente manera;

4, 2, 1,..., ∞

2) La suma de 'n' términos de una progresión geométrica hasta el infinito para -1 <r <1 se da como sigue;

`S_(\infty) = (a)/(1 - r)`

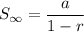
Por lo tanto, la suma de las áreas de los cuadrados hasta el infinito se obtiene sustituyendo los valores de 'a' y 'r' en la ecuación anterior de la siguiente manera;

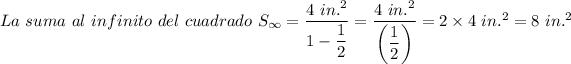
`La \ suma \ al \ infinito \ del \ cuadrado \ S_(\infty) = (4 \ in.^2)/(1 - (1)/(2) ) = (4 \ in.^2)/(\left((1)/(2) \right)) = 2 * 4 \ in.^2= 8 \ in.^2`

La suma al infinito de las áreas de los cuadrados,
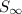`S_(\infty)` = 8 in.²