Question

.4^3Grafting, the uniting of the stem of one plant with the stem or root of another, is widely used commercially to grow the stem of one variety that produces fine fruit on the root system of another variety. Suppose grafts are done one at a time. A graft fails with probability 0.4, independently of the others. Given there were no failed grafts in the first seven done, what is the probability that there will be at least one failed graft in the next three done

Answer 1

0.784 = 78.4% probability that there will be at least one failed graft in the next three done

Explanation:

To solve this question, we need to understand the binomial probability distribution and conditional probability.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: No failed grafts in the first seven

Event B: At least one fail in the next three.

Intersection of events A and B:

Since the probability of a graft failling is independent of other grafts, we have that:

`P(A \cap B) = P(A)*P(B)`

So

`P(B|A) = (P(A \cap B))/(P(A)) = (P(A)*P(B))/(P(A)) = P(B)`

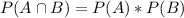
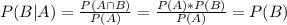
So we just have to find the probability of one fail in three trials.

Three trials means that
`n = 3`.

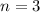The probability is

`P(X \geq 1) = 1 - P(X = 0)`

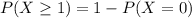
In which

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(3,0).(0.4)^(0).(0.6)^(3) = 0.216`

Then

`P(X \geq 1) = 1 - P(X = 0) = 1 - 0.216 = 0.784`

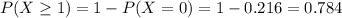
0.784 = 78.4% probability that there will be at least one failed graft in the next three done