Answer:
The hammer reaches the river after 15.8 seconds.
Explanation:
The formula to find for how long it takes for the hammer to reach the ground is given by:
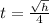
In which h is the initial height.
A construction worker drops a hammer while building the Grand Canyon skywalk 4,000ft above the Colorado River.
This means that
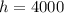 .
.
So
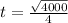
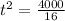
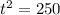
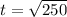
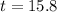
The hammer reaches the river after 15.8 seconds.