Answer:
The mean of the sampling distribution of p is 0.25 and the standard deviation is 0.0685.
Explanation:
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
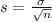 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
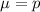 and standard deviation
and standard deviation
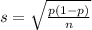
25% of the approximately 1000 issues reported per month that require more than one call.
This means that
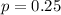
What are the mean and standard deviation of the sampling distribution of p?
Sample of 40 means that
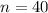 .
.
By the Central Limit Theorem,
The mean is

The standard deviation is
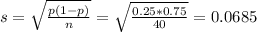
The mean of the sampling distribution of p is 0.25 and the standard deviation is 0.0685.