Answer:
Amanda buy first kind of pen = 3
Amanda buy second kind of pen = 2
Amanda buy third kind of pen = 15
Explanation:
Given - Amanda went to the store to purchase ink pens. She found three
kinds of pens. The first cost $4 each; the price of the second kind
was 4 for $1; and the cost for the third kind was 2 for $1. She bought
20 pens and she bought at least one of each kind. (It is possible to
buy only 1 of the pens that are "4 for $1" or "2 for $1".) The cost was
$20.
To find - When she got back to her office, Amanda decided to turn this into
a math problem for me. She asked: how many of each kind did I
buy?
Proof -
Let Amanda buy first kind of pen = x
second kind of pen = y
third kind of pen = z
As given,
She bought total pen = 20
⇒x + y + z = 20 ...............(1)
Now,
As given,
cost for first kind pen = $4 for 1 pen
As she bought x pens of first kind , so
Cost of x pens of first kind = $4x
Now,
The price of the second kind was 4 for $1
⇒Cost of second kind = $
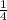for 1 pen
As she bought y pens of send kind , so
Cost of y pens of second kind = $
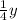
Now,
The price of the third kind was 2 for $1
⇒Cost of third kind = $
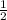for 1 pen
As she bought z pens of send kind , so
Cost of z pens of third kind = $
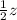
Now,
As given, The cost was $20
⇒4x +
+
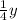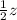= 20
⇒16x + y + 2z = 80 .....................(2)
∴ we get 2 equations
x + y + z = 20 .....................(1)
16x + y + 2z = 80 .....................(2)
Now,
Subtract equation (1) from equation (2) , we get
16x + y + 2z - ( x+ y + z )= 80 - 20
⇒16x + y + 2z - x - y - z = 60
⇒15x + z = 60
⇒z = 60 - 15x
Now,
Put the value of z in equation (1) , we get
x + y + 60 - 15 x = 20
⇒ y - 14x = 20 - 60
⇒y - 14x = -40
⇒14x - y = 40
⇒y = 14x - 40
Now,
we get
z = 60 - 15x
y = 14x - 40
As given
she bought at least one of each kind
it means x > 1, y > 1, z > 1
Now,
If x = 1, then y = 14 - 40 = -26
Not possible
If x = 2 , then y = 14(2) - 40 = -12
Not possible
If x = 3, then y = 14(3) - 40 = 2 and z = 60 - 15(3) = 15
Possible.
If x = 4, then y = 14(4) - 40 = 16 and z = 60 - 15(4) = 0
Not Possible.
If x = 5, then y = 14(5) - 40 = 30 and z = 60 - 15(5) = -15
Not Possible.
∴ we get
x = 3, y = 2, z = 15
Amanda buy first kind of pen = x = 3
Amanda buy second kind of pen = y = 2
Amanda buy third kind of pen = z = 15