Question

Which best describes the transformation that occurs from the graph of f(x) = x2 to g(x) = (x 3)2 4?left 3, up 4right 3, down 4left 3, down 4right 3, up 4

Answer 1

Right 3, Down 4

Explanation:

Given

`f(x) = x^2`

`g(x) = (x + 3)^2 - 4`

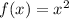
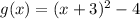
Required

The transformation from f(x) to g(x)

When a function is translated up by h units, the rule is:

`(x,y) \to (x + h,y)`

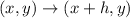
So, we have:

`f'(x) = (x + h)^2`

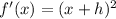
By comparison, h = 3. So:

`f'(x) = (x + 3)^2`

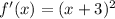
When a function is translated down by h units, the rule is:

`(x,y) \to (x,y - h)`

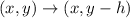
So, we have:

`g(x) = f'(x) -h`

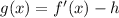
By comparison, h = 4. So:

`g(x) = (x + 3)^2 - 4`

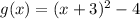
Hence, the transformation is: 3 units right and 4 units down