Question

At a dock on the east coast, low tide occurs at 3 pm wi th a water depth of 5 ft. The depth at high tide is 83 ft. High tide occurs every 6 hours. Explain how to find the sinusoidal function that models the depth in terms of time, x.

Answer 1

The sinusoidal function that model the depth in terms of time, 'x', is presented here as follows;

f(x) = 39·sin((π/3)·x - π) + 5

Explanation:

A sinusoidal function is given by the general function as follows;

y = A·sin(B·x + C) + D

Where;

A = The amplitude = (
`y_(max)` -
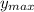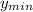`y_(min)`)/2 = (The high tide - The low tide)/2 = (83 ft. - 5 ft.)/2 = 39 ft.

The period, T = 2·π/b = 6 hours

∴ B = 2·π/T = 2·π/6 = π/3

D = The vertical shift = The low tide = 5 ft.

The horizontal phase shift, 'C', is given as follows;

3 hrs = -C/B = -C/(π/(3 hr))

C = 3 hrs × -(π/(3 hr)) = -π

∴ C = -π

y = 39·sin((π/3)·x - π) + 5

The sinusoidal function that model the depth in terms of time, 'x', is therefore given as follows;

f(x) = 39·sin((π/3)·x - π) + 5