Answer:
13.759 % of the initial mechanical energy is lost as thermal energy.
Step-by-step explanation:
By the First Law of Thermodynamics we know that increase in internal energy of the object (
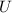 ), in joules, is equal to the lost amount of the change in gravitational potential energy (
), in joules, is equal to the lost amount of the change in gravitational potential energy (
 ), in joules:
), in joules:
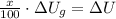 (1)
(1)
Where
 is the percentage of the energy loss, no unit.
is the percentage of the energy loss, no unit.
By definition of the gravitational potential energy and internal energy, we expand this equation:
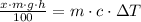 (1b)
(1b)
Where:
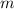 - Mass of the object, in kilograms.
- Mass of the object, in kilograms.
 - Gravitational acceleration, in meters per square second.
- Gravitational acceleration, in meters per square second.
 - Initial height of the object above the lunar ground, in meters.
- Initial height of the object above the lunar ground, in meters.
 - Specific heat of aluminium, in joules per degree Celsius-kilogram.
- Specific heat of aluminium, in joules per degree Celsius-kilogram.
 - Temperature increase due to collision, in degree Celsius.
- Temperature increase due to collision, in degree Celsius.
If we know that
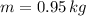 ,
,
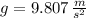 ,
,
 ,
,
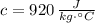 and
and
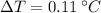 , then the percentage of energy loss due to collision is:
, then the percentage of energy loss due to collision is:
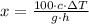
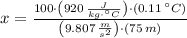
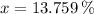
13.759 % of the initial mechanical energy is lost as thermal energy.