Answer:
The parabola is negative, with a vertex at (7, -7) and a line of symmetry at x = 7
Explanation:
A parabola is set of all points in a plane which are an equal distance away from a given point (focus) and given line (directrix).
Let
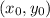 be any point on the parabola.
be any point on the parabola.
Find an equation for the distance between
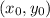 and the focus.
and the focus.
Find an equation for the distance between
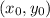 and directrix. Equate these two distance equations, simplify, and the simplified equation in
and directrix. Equate these two distance equations, simplify, and the simplified equation in
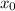 and
and
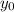 is equation of the parabola.
is equation of the parabola.
Distance between
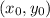 and the focus (7, -11):
and the focus (7, -11):
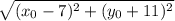
Distance between
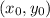 and the directrix, y = -3:
and the directrix, y = -3:
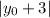
Equate the two distance expressions and simplify, making
 the subject:
the subject:
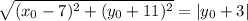
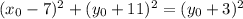
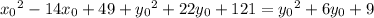
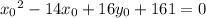
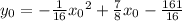
This equation in
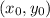 is true for all other values on the parabola so we can rewrite with
is true for all other values on the parabola so we can rewrite with
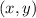
Therefore, the equation of the parabola with focus (7, -11) and directrix is y = -3 is:
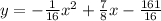
⇒
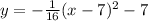 (in vertex form)
(in vertex form)
So the parabola is negative, with a vertex at (7, -7) and a vertical line of symmetry at x = 7