Question

From rest, we step on the gas of our Ferrari, providing a force F for 4secs, speed up to a final speed v. If the applied force were only 1/2 F, how long would it have to be applied to reach the same final speed?

Answer 1

The force must be applied during 8 seconds to reach trhe same final speed.

Step-by-step explanation:

By Impulse Theorem, a change in the magnitude of linear momentum of a system with constant mass can be done by applying a force during a given time. That is:

`m\cdot (v_(f)-v_(o)) = F \cdot \Delta t`

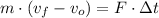
Where:

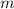`m` - Mass, measured in kilograms.

`v_(o)`,
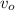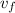`v_(f)` - Initial and final speed, measured in meters per second.

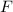`F` - Net external foce, measured in newtons.

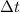`\Delta t` - Time, measured in seconds.

We can eliminate mass and speeds by constructing the following relationship:

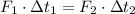`F_(1)\cdot \Delta t_(1) = F_(2)\cdot \Delta t_(2)` (2)

If we know that
`F_(1) = F`,
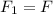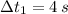`\Delta t_(1) = 4\,s` and
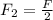`F_(2) = (F)/(2)`, then the time is:

`4\cdot F = (F\cdot \Delta t_(2))/(2)`

`\Delta t_(2) = 8\,s`

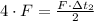
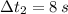
The force must be applied during 8 seconds to reach trhe same final speed.