Question

The masses of astronauts are monitored during long stays in orbit, such as when visiting a space station. The astronaut is strapped into a chair that is attached to the space station by springs and the period of oscillation of the chair in a friction-less track is measured.

(a) The period of oscillation of the 10.0 kg chair when empty is 0.750 s. What is the effective force constant of the springs?
(b) What is the mass of an astronaut who has an oscillation period of 2.00 s when in the chair?
(c) The movement of the space station should be negligible. Find the maximum displacement of the 100,000 kg sace station if the astronaut's motion has an amplitude of 0.100 m.

Answer 1

a) k = 701.8 N / m, b) m_{ast} = 61.1 kg, c) v ’= -1.3 10⁻⁴ m / s

Step-by-step explanation:

a) For this exercise let's use the relationship of the angular velocity

w =
`\sqrt{ (k)/(m) }`

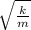
k = w² m

the angular velocity is related to the period

w = 2π / T

we substitute

k = 4 π²
`(m)/(T^2)`

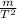
let's calculate

k = 4 π² 10 /0.75²

k = 701.8 N / m

b) now repeat the measurement with an astronaut on the chair

w =
`\sqrt{ (k)/(m) }`

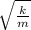
where the mass Month the mass of the chair plus the mass of the astronaut

M = m +
`m_(ast)`

M = k / w²

w = 2π / T

let's calculate

w = 2π / 2

w = π rad / s

M = 701.8 /π²

M = 71,111 kg

now we use that

M = m + m_{ast}

m_{ast} = M - m

m_{ast} = 71.111 - 10.0

m_{ast} = 61.1 kg

c) if the astronaut's movement is simple harmonic

x = A cos wt

therefore the speed is

v =
`(dx)/(dt)`

v = -Aw sin wt

maximum speed is

v = - Aw

v = 0.100 π

v = 0.31416 m / s

we can suppose that the movement of the space station and the astronaut is equivalent to division of the same

initial instant. Before the move

p₀ = 0

final instant. When the astronaut is moving

p_f = M_station v’+ m_{ast} v

the moment is preserved

p₀ = pf

0 = M__{station} v ’+ m_{ast} v

v ’= -
`(m_(ast) )/(M_(station) ) \ v`

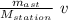
we substitute

v ’=
`(61.1 )/( 100000 ) \ 0.31416`

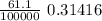
v ’= -1.3 10⁻⁴ m / s

the negative sign indicates that the station is moving in the opposite direction from the astronaut