Question

A ball is thrown vertically with a velocity of18 m/s. It’s height, h, in meters above the ground after t seconds is given by the equation: h= -5t2+10t+35. Algebraically, determine the following.

Find The maximum height of the ball and the time it takes to reach that height
The time it takes the ball to hit the ground.

PLEASE HELP!

Answer 1

Explanation:

First of all, something is wrong with either the wording in the problem or the equation that you wrote; if the upward velocity is 18, we should see 18t in the equation, not 10t. I solved using 10t.

To find the max height of the ball and the time it took to get there, we need to complete the square on this quadratic and solve for the vertex. That will give us both of those answers in one!

To complete the square, set the quadratic equal to 0 and then move over the constant, like this:

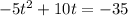`-5t^2+10t=-35` The rule is that we have to have a 1 as the leading coefficient, and right now it's a -5, so we factor that out, leaving us with:

`-5(t^2-2t)=-35` and now we are ready to begin the process to complete the square.

The rule is: take half the linear term, square it, and add it to both sides. Our linear term is a -2 (from the -2t); half of -2 is -1, and -1 squared is 1. We add in a one to both sides. BUT when we put the 1 into the set of parenthesis on the left, we didn't just add in a 1, we have that -5 out front that is a multiplier. That means that we actually added in a -5 after it's all said and done.

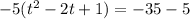`-5(t^2-2t+1)=-35-5` and we'll clean that up a bit. The right side is easy, that's a -40. The left side...not so much.

The reason we complete the square is to put this quadratic into vertex form. Completing the square creates a perfect square binomial on the left, which for us is, along with the simplification on the right:

`-5(t-1)^2=-40`

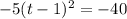
Lastly, we move the -40 back over by adding and setting the quadratic back to equal y:

`-5(t-1)^2+40=y` and we see that the vertex is (1, 40). That translates to a height of 40 meters at 1 second after launch. That's the vertex which, by definition, is the max or min of the parabola. Because our parabola is negative, the vertex for us is a max.

To find out how long it takes the ball to hit the ground, set the quadratic equal to 0 and factor however it is you are currently doing this in class. You can continue to factor from the vertex form we have the equation in if you'd like. Let's do that, since we are already most of the way there. Begin here:

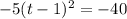`-5(t-1)^2=-40` and divide both sides by -5 to get

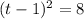`(t-1)^2=8` and take the square root of both sides to "undo" that squaring on the left:

t - 1 = ±√8. Now add 1 to both sides to isolate the t:

t = 1 ± √8. In decimal form:

t = 1 + √8 is 3.828 seconds and

t = 1 - √8 is -1.828 seconds.

Since we all know that time will NEVER be a negative value, the time it takes the ball to hit the ground is 3.828 seconds.