Answer:
The distance (in miles) by the bus up the hill when its speed decreased to 50 mph is approximately 1.353 miles
Step-by-step explanation:
The parameters of the motion of the driver are;
The upgrade of the road, θ = 10°
The rate of constant acceleration of the bus driver = 5 ft./s²
The speed of the bus as it begins to go up the hill, v₁ = 80 mph = 117.3228 ft./s
The speed of the driver at a point on the hill, v₂ = 50 mph ≈ 73.32677 ft./s
The acceleration due to gravity, g ≈ 32.1740 ft./s²
Therefore, we have;
The acceleration due to gravity down the incline plane, gₓ = g·sinθ
∴ gₓ = g·sin(θ) ≈ 32.1740 ft./s² × sin(10°) ≈ 5.587 ft/s²
The net acceleration of the bus, on the incline plane,
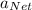 = gₓ - a = 5.587 ft./s² -5 ft./s² = 0.587 ft./s²
= gₓ - a = 5.587 ft./s² -5 ft./s² = 0.587 ft./s²
The vertical component of the velocity,
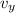 = v × sin(θ)
= v × sin(θ)
∴
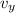 = 117.3228 ft./s × sin(10°) ≈ 20.37289 ft./s
= 117.3228 ft./s × sin(10°) ≈ 20.37289 ft./s
vₓ = 117.3228 ft./s × cos(10°) ≈ 115.5404 ft./s
The velocity of the car, v₂, on the inclined plane is given as follows;
v₂ = v₁ -
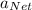 × t
× t
∴ t = (v₁ - v₂)/
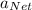 = (117.3228 ft./s - 73.32677 ft./s)/(0.587 ft./s²) ≈ 74.95 s
= (117.3228 ft./s - 73.32677 ft./s)/(0.587 ft./s²) ≈ 74.95 s
The distance covered, 's', is given as follows;
s = v₁·t - 1/2·
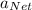 ·t²
·t²
∴ s = 117.3228 × 74.95 - 1/2 × 0.587 × 74.95² ≈ 7144.6069 ft.
The distance travelled up the hill, s ≈ 7144.6069 ft. ≈ 1.3531452 miles ≈ 1.353 miles