Question

A line passes through the points (1, -4) and (3, 2). Write the equation of the line in the slope-intercept form.

Answer 1

`y=3x-7`

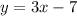
Explanation:

Hi there!

Slope-intercept form:
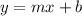`y=mx+b` where m is the slope and b is the y-intercept (the value of y when x is 0)

1) Determine the slope (m)

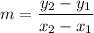`$m=(y_2-y_1)/(x_2-x_1)` where two given points are
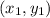`(x_1,y_1)` and
`(x_2,y_2)`

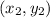
Plug in the given points (1, -4) and (3, 2):

`\displaystyle m=(2-(-4))/(3-1)\\\\\displaystyle m=(2+4)/(3-1)\\\\\displaystyle m=(6)/(2)\\\\\displaystyle m=3`

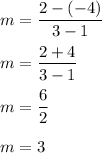
Therefore, the slope of the line is 3. Plug this into
`y=mx+b`:

`y=3x+b`

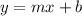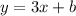
Normally, we would now go about solving for the y-intercept and forming the possible equation for this line. However, there is only one choice option that has 3 as the slope. Therefore, the equation of the line must be
`y=3x-7`.

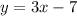I hope this helps!