Answer:
The 95% confidence interval estimate of the difference between the proportion of women and men who think sexual harassment is a major problem in the American workplace is (0.2824, 0.4776). The upper limit of the confidence interval is 0.4776.
Explanation:
Before solving this question, we need to understand the central limit theorem and subtraction of normal variables.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
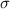 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
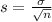 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
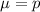 and standard deviation
and standard deviation
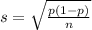
Subtraction between normal variables:
When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.
Proportion of women:
62% of 150, so:
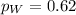
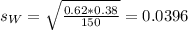
Proportion of men:
24% of 200, so:


Distribution of the difference:
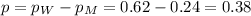
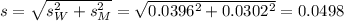
Confidence interval:
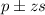
In which
z is the z-score that has a p-value of
 .
.
95% confidence level
So
 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
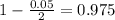 , so
, so
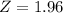 .
.
The lower limit of this interval is:

The upper limit of this interval is:
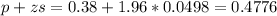
The 95% confidence interval estimate of the difference between the proportion of women and men who think sexual harassment is a major problem in the American workplace is (0.2824, 0.4776). The upper limit of the confidence interval is 0.4776.