Answer:
- WX =
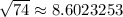
- XY =
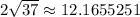
- WY =
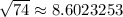
- Classify: Isosceles
============================================================
Step-by-step explanation:
Apply the distance formula to find the length of segment WX
W = (x1,y1) = (-10,4)
X = (x2,y2) = (-3, -1)
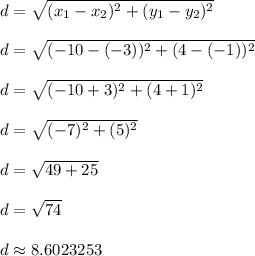
Segment WX is exactly
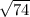 units long which approximates to roughly 8.6023253
units long which approximates to roughly 8.6023253
-------------------
Now let's find the length of segment XY
X = (x1,y1) = (-3, -1)
Y = (x2,y2) = (-5, 11)
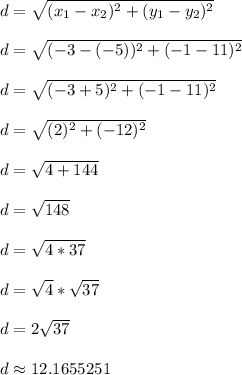
Segment XY is exactly
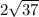 units long which approximates to 12.1655251
units long which approximates to 12.1655251
-------------------
Lastly, let's find the length of segment WY
W = (x1,y1) = (-10,4)
Y = (x2,y2) = (-5, 11)
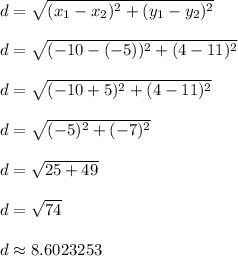
We see that segment WY is the same length as WX.
Because we have exactly two sides of the same length, this means triangle WXY is isosceles.