Question

At which root does the graph of f(x) = (x + 4)^6(x + 7)^5 cross the x-axis?

O -7
O -4
O 4
Ο 7

Answer 1

Step-by-step explanation:

to cross the x-axis you need to solve f(x)=0

x(x+4)(x+7)*5=0 which means you will have x=0 ,x+4=0 or x+7=0

so the final answer is

x=0 or x=-4 or x=-7

Answer 2

The graph of
`f(x) = (x + 4)^6(x + 7)^5` crosses the x-axis at the roots x = -4 and x = -7.

The answer is option ⇒ 1 and 2

Step-by-step explanation:

To find the roots of the equation
`f(x) = (x + 4)^6(x + 7)^5`, we need to determine the values of x that make the function equal to zero and intersect the x-axis.

To do this, we set f(x) equal to zero and solve for x:

`(x + 4)^6(x + 7)^5 = 0`

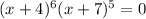
We know that a product of factors is equal to zero if and only if at least one of the factors is equal to zero.

Setting each factor equal to zero, we have:

x + 4 = 0 (Root 1)

x + 7 = 0 (Root 2)

Solving for x in each equation, we find:

Root 1: x = -4

Root 2: x = -7

Therefore, the graph of
`f(x) = (x + 4)^6(x + 7)^5` crosses the x-axis at the roots x = -4 and x = -7.

To summarize:

- The graph of
`f(x) = (x + 4)^6(x + 7)^5` crosses the x-axis at the roots x = -4 and x = -7.

The answer is option ⇒ 1 and 2