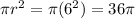2 Answers

Linette · Answer 1 · 2022-06-15T20:47:32+0000

Answer:

$36\pi$

Explanation:

The diameter is:

The Euclidean distance between points (x1, y1) and (x2, y2) is:

sqrt((x1 - x2)^2 + (y1 - y2)^2)

Substitute (x1, y1) = (0, 4) and (x2, y2) = (0, -8):

= sqrt((-0 + 0)^2 + (-(-8) + 4)^2)

= sqrt(12^2)

= 12

or simply:

diameter: 4-(-8)=12

The radius is:

12/2=6 units

The area of the circle:

$\pi r^2=\pi(6^2)=36\pi$

Please log in or register to add a comment.