Answer:
a)
 inches
inches
The sampling distribution of the sample means annual rainfall for California is 1.278.
b)
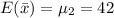 inches
inches
The sampling distribution of the sample means annual rainfall for New York is 1.0435.
c)
Here, The standard error of New York is smaller because the sample size is larger than for California.
Explanation:
California:
 inches.
inches.
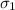 = 7 inches.
= 7 inches.
 = 30 years.
= 30 years.
New York:
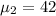 inches.
inches.
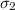 = 7 inches.
= 7 inches.
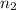 = 45 years.
= 45 years.
a)
 inches
inches
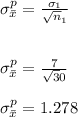
b)
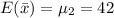 inches
inches
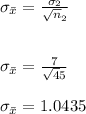
c)
Here, The standard error of New York is smaller because the sample size is larger than for California.