Question

The state of California has a mean annual rainfall of 22 inches, whereas the state of New York has a mean annual rainfall of 42 inches. Assume that the standard deviation for both states is 7 inches. A sample of 30 years of rainfall for California and a sample of 45 years of rainfall for New York has been taken.

(a) Show the sampling distribution of the sample mean annual rainfall for California.
(b) Show the sampling distribution of the sample mean annual rainfall for New York.
(c) In which of the preceding two cases, part (a) or part (b), is the standard error of x smaller? Why?
The standard error is [larger, smaller] for New York because the sample size is [larger, smaller] than for California.

Answer 1

a)
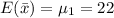`E(\bar x) = \mu_(1) = 22` inches

The sampling distribution of the sample means annual rainfall for California is 1.278.

b)

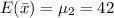`E(\bar x) = \mu_(2) = 42` inches

The sampling distribution of the sample means annual rainfall for New York is 1.0435.

c)

Here, The standard error of New York is smaller because the sample size is larger than for California.

Explanation:

California:

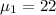`\mu_(1) = 22` inches.

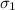`\sigma_(1)` = 7 inches.

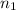`n_(1)` = 30 years.

New York:

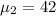`\mu_(2) = 42` inches.

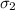`\sigma_(2)` = 7 inches.

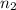`n_(2)` = 45 years.

a)

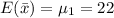`E(\bar x) = \mu_(1) = 22` inches

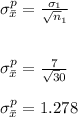
`\sigma^(p) _(\bar x) = (\sigma_(1) )/(\sqrt n_(1) ) \\\\\\\sigma^(p) _(\bar x) = (7)/(\sqrt 30) \\\\\sigma^(p) _(\bar x) = 1.278`

b)

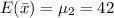`E(\bar x) = \mu_(2) = 42` inches

`\sigma _(\bar x) = (\sigma_(2) )/(\sqrt n_(2) ) \\\\\\\sigma_(\bar x) = (7)/(\sqrt45) \\\\\sigma _(\bar x) = 1.0435`

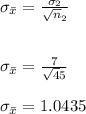
c)

Here, The standard error of New York is smaller because the sample size is larger than for California.