Question

Write an equation in slope-intercept form for the line that passes through the given point and is parallel to the graph of the equation.

(4,−3); y=3x−5

Answer 1

`y=3x-15`

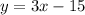
Explanation:

Slope intercept form:
`y=mx+b` where
`m` is the slope and
`b` is the y-intercept (the value of y when the line crosses the y-axis)

1) Find the slope of the line (
`m`)

When it comes to parallel lines, they will always have the same slope but different y-intercepts. The given equation is
`y=3x-5`. Because 3 is in the place of m, we know that the slope of the line is 3. Therefore, the slope of the line parallel to it will also be 3. So far, this is what our equation looks like:

`y=3x+b`

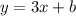
2) Find the y-intercept (
`b`)

To find the y-intercept, we plug the given point (4,-3) into the equation we currently have and solve for b.

`y=3x+b\\-3=3(4)+b\\-3=12+b`

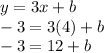
Subtract both sides by 12

`-3-12=12+b-12\\-15=b`

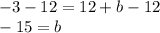
Therefore the y-intercept of our line is -15. Plug -15 back into the original equation as b.

`y=3x+(-15)\\y=3x-15`

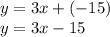
I hope this helps!