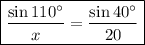Question

Plzzz need help steps if possible just plzz dont ignore plzzzz

Answer 1

I think it is either B or C

Sorry if it is wrong

Explanation:

Answer 2

`\text{(D) }(\sin 110^(\circ))/(x)=(\sin 40^(\circ))/(20)`

Explanation:

We can use the Law of Sines to solve this problem. The Law of Sines works for any triangle and states that the ratio of any angle and its opposite side is maintained throughout all angles of the triangle:

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

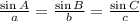
In the figure, the angle marked 110 degrees has an opposite side labelled
`x`. However, the angle opposite to the side marked 20 is still unknown, so let's find it.

The sum of the interior angles of a triangle is always 180 degrees. Therefore, let the third angle be
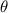`\theta`. We have:

`\theta + 110^(\circ)+30^(\circ)=180^(\circ),\\\theta+140^(\circ)=180^(\circ),\\\theta=40^(\circ)`

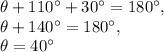
Now we have the relevant angle and we can set up the proportion:

`\boxed{(\sin 110^(\circ))/(x)=(\sin 40^(\circ))/(20)}`