Question

.

A football is punted from a height of 2.75 ft above the ground, with an initial velocity of 48 feet per
second. The motion of the football can be modeled by the equation h = -16t2 + 48t +2.75, where
h represents the height of the football, in feet, and t represents the timelin seconds.
If the football is caught 5.25 ft above the ground, approximately how long did it remain in the air?
Roundyour answer to the nearest hundredth of a second.

Answer 1

Explanation:

The position function for this is given as

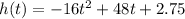`h(t)=-16t^2+48t+2.75` where h(t) is the height of the football at any time t. If the ball is caught at 5.25 feet, that h(t) value is 5.25 since we are looking for the time the ball was in the air from its initial 2.75 feet to 5.25 feet, when it was caught.

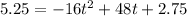`5.25=-16t^2+48t+2.75` and set this equal to 0:

`-16t^2+48t-2.5=0` and factor.

When we factor we get

t = .05 and t = 2.95 in seconds.

That first time tell us how long it takes to go from the initial height of 2.75 to a point 2.5 feet higher, 5.25. To get get back down to the 5.25 foot height on the other side of the vertex, is 2.95 seconds. So the total time the ball was in the air was 3 seconds exactly.