We are given the slope of the line and a point that it passes through.
So, we can use the Point-Slope Formula:
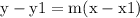
Where y1 is the y-coordinate of the point, m is the slope of the line, and x1 is the x-coordinate of the line.
Now, plug in the values:
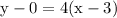
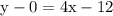
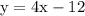 (the equation of the line in slope-intercept form)
(the equation of the line in slope-intercept form)
Now, how to graph it?
First of all, the y-intercept is (0, -12)
Remember, y-intercepts always have an x-coordinate of 0.
Now, 4 is the slope (Rise/Run)
Where Rise is how many units we move up or down, and Run is how many units we move left or right.
In this case, we move 4 up, over 1, up 4, over 1, and so on, until we have a line.
Then all we have to do is take a ruler and connect the points. :)
Hope you find it helpful.
Feel free to ask if you have any doubts.