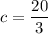Question

What is the value of c in the interval (5,8) guaranteed by Rolle's Theorem for the function g(x)=−7x3+91x2−280x−9? Note that g(5)=g(8)=−9. (Do not include "c=" in your answer.)

Answer 1

`\displaystyle c = (20)/(3)`

Explanation:

According to Rolle's Theorem, if f(a) = f(b) in an interval [a, b], then there must exist at least one c within (a, b) such that f'(c) = 0.

We are given that g(5) = g(8) = -9. Then according to Rolle's Theorem, there must be a c in (5, 8) such that g'(c) = 0.

So, differentiate the function. We can take the derivative of both sides with respect to x:

`\displaystyle g'(x) = (d)/(dx)\left[ -7x^3 +91x^2 -280x - 9\right]`

Differentiate:

`g'(x) = -21x^2+182x-280`

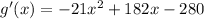
Let g'(x) = 0:

`0 = -21x^2+182x-280`

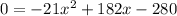
Solve for x. First, divide everything by negative seven:

`0=3x^2-26x+40`

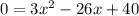
Factor:

`0=(x-2)(3x-20)`

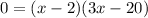
Zero Product Property:

`x-2=0 \text{ or } 3x-20=0`

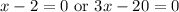
Solve for each case. Hence:

`\displaystyle x=2 \text{ or } x = (20)/(3)`

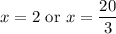
Since the first solution is not within our interval, we can ignore it.

Therefore:

`\displaystyle c = (20)/(3)`