Answer:
Center: ( -1 , 2 )
Radius: 6
Explanation:
The equation for a circle is given as follow:
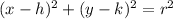
Where,
the Center is: ( h , k ) (note that the signs of the number are different)
and the radius is: r
So if we compare the original circle equation to the equation in the question we can see that:
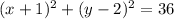
the Center is: (-1,2)
and the radius is:
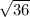 = 6
= 6
2. To draw the graph find points that lay on the circle, it's better to take the values of x and y from the Center:
first sub y=2 in the equation to find the values for x:
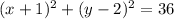
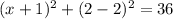


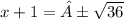
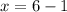 AND
AND
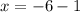
 AND
AND
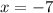
- The points are A(5,2) and B(-7,2)
second sub x= -1 in the equation to find the values for y:
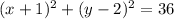
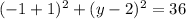

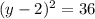
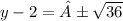
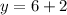 AND
AND
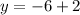
 AND
AND
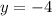
- The points are D(-1,8) and E(-1,-4)
After finding the points write them in the graph and match them together to get the like the circle in the picture below: