1 Answer

CiNN · Answer 1 · 2022-05-13T12:37:14+0000

Answer:

The proof is done in the step-by-step explanation below.

Explanation:

We are given the following identity:

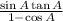
(sin(A)tan(A))/(1-cos(A))

And we have to show that this is equals to:

$1 + \sec{A}$

Multiplying numerator and denominator by the conjugate of the denominator:

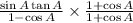
(sin(A)tan(A))/(1-cos(A)) * (1+cos(A))/(1+cos(A))

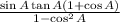
$\frac{sin(A)tan(A)(1+cos(A))}{1 - \cos^2{A}}$

We use these following identities:

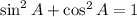
$\sin^2{A} + \cos^2{A} = 1$

So

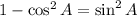
$1 - \cos^2{A} = \sin^2{A}$

Also:

tan(A) = (sin(A))/(cos(A))

Then

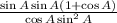
$\frac{sin(A)sin(A)(1+cos(A))}{cos(A)\sin^2{A}}$

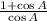
$\frac{\sin^2{A}(1+cos(A))}{cos(A)\sin^2{A}}$

(1 + cos(A))/(cos(A))

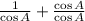
(1)/(cos(A)) + (cos(A))/(cos(A))

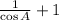
(1)/(cos(A)) + 1

Since:

$\sec{A} = (1)/(cos(A))$

We have that:

$1 + \sec{A}$

Thus, the proof is done.

Please log in or register to add a comment.