Answer:
1)
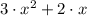 - The polynomial expression is a second-grade binomial, with a coefficient of 3 on the second-grade monomial component and a coefficient of 2 on the first-grade monomial component.
- The polynomial expression is a second-grade binomial, with a coefficient of 3 on the second-grade monomial component and a coefficient of 2 on the first-grade monomial component.
2)
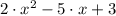 - The polynomial expression is a third-grade trinomial, with a coefficient of 2 on the second-grade monomial component, a coefficient of -5 on the first-grade monomial component and a coeffcient of 3 on the zero-grade monomial component.
- The polynomial expression is a third-grade trinomial, with a coefficient of 2 on the second-grade monomial component, a coefficient of -5 on the first-grade monomial component and a coeffcient of 3 on the zero-grade monomial component.
3)
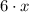 - The polynomial expression is a first-grade monomial, with a coefficient of 6 on the first grade monomial component.
- The polynomial expression is a first-grade monomial, with a coefficient of 6 on the first grade monomial component.
Explanation:
1)
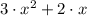 - The polynomial expression is a second-grade binomial, with a coefficient of 3 on the second-grade monomial component and a coefficient of 2 on the first-grade monomial component.
- The polynomial expression is a second-grade binomial, with a coefficient of 3 on the second-grade monomial component and a coefficient of 2 on the first-grade monomial component.
2)
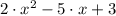 - The polynomial expression is a third-grade trinomial, with a coefficient of 2 on the second-grade monomial component, a coefficient of -5 on the first-grade monomial component and a coeffcient of 3 on the zero-grade monomial component.
- The polynomial expression is a third-grade trinomial, with a coefficient of 2 on the second-grade monomial component, a coefficient of -5 on the first-grade monomial component and a coeffcient of 3 on the zero-grade monomial component.
3)
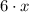 - The polynomial expression is a first-grade monomial, with a coefficient of 6 on the first grade monomial component.
- The polynomial expression is a first-grade monomial, with a coefficient of 6 on the first grade monomial component.