Question

find the component equation of the plane which is normal to the vector -2i+5j+k and which contains the point (-10;7;5).​

Answer 1

Given:

A plane is normal to the vector = -2i+5j+k

It contains the point (-10,7,5).​

To find:

The component equation of the plane.

Solution:

The equation of plane is

`a(x-x_0)+b(y-y_0)+c(z-z_0)=0`

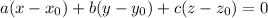
Where,
`(x_0,y_0,z_0)` is the point on the plane and
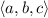`\left< a,b,c\right>` is normal vector.

Normal vector is -2i+5j+k and plane passes through (-10,7,5). So, the equation of the plane is

`-2(x-(-10))+5(y-7)+1(z-5)=0`

`-2(x+10)+5y-35+z-5=0`

`-2x-20+5y-35+z-5=0`

`-2x+5y+z-60=0`

`-2x+5y+z=60`

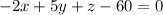
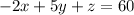
Therefore, the equation of the plane is
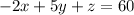`-2x+5y+z=60`.