Answer:
n = 50
Explanation:
Let a be the first term and d be the common difference.
An arithmetic sequence has a 2nd term equal to 3 and 10th term equal to -13.

According to the given condition,
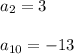
or
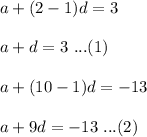
Subtract equation (1) from (2).
a+9d-(a+d) = -13-3
8d = -16
d = -2
Put the value of d in equation (1).
a+(-2) = 3
a = 3+2
a = 5
Now,
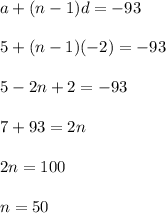
So, 50th term has the value of -93.