Given:
Lavro sells 320 sausages per day at a price of $5.50 each.
The previous year's sales show that for every $0.50 decrease in price, he will sell another 40 sausages.
The equation that models this problem is:

To find:
The maximum potential revenue.
Solution:
We have,

It can be written as:
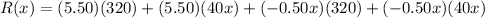
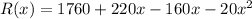

Differentiate with respect to x.
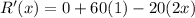
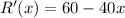
For critical points,
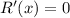 .
.
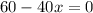
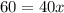
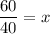
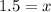
Differentiate R'(x) with respect to x.
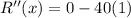
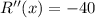
Since R''(x)<0, therefore function R(x) is maximum at
 . The maximum value is:
. The maximum value is:
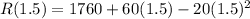
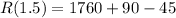
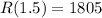
Therefore, the maximize potential revenue is $1805 at
 .
.